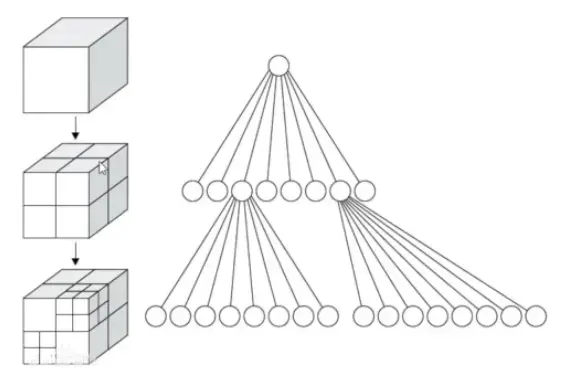
如果整个3D模型用一个长方体空间来表示，在三维空间xyz三个方向，都分割一次，这样就可以得到8个小的长方体子空间。

一个3D模型的三角形（项点）分布在三维空间中，如果你用一个长方体来表示整个3d场景，当你分割为8个子空间的时候，每个子空间可以包含对应的三角形（顶点）数据。

每个子空间如果三角形（项点）数量比较多，还可以继续分割，具体分割规则，你可以自定义，比如你可以规定，一个子空间包含的三角形数量只要大于8个就继续分割。这样一个个子空间可以构成一个树结构，整体来看，每个节点，分叉出来八个子节点。

八叉树（Octree）是一种用于描述三维空间的树状数据结构。每个节点表示一个正方体的体积元素，每个节点有八个子节点，这八个子节点所表示的体积元素加在一起就等于父节点的体积。八叉树结构通过对三维空间的几何实体进行体元剖分，每个体元具有相同的时间和空间复杂度，通过循环递归的划分方法对大小为\(2^n*2^n*2^n\)的空间进行划分。

八叉树的实现原理如下：

1. 设定最大递归深度。
2. 找出场景的最大尺寸，并以此尺寸建立第一个立方体。
3. 依序将单位元元素丢入能被包含且没有子节点的立方体。
4. 若没有达到最大递归深度，就进行细分八等份，再将该立方体所装的单位元元素全部分担给八个子立方体。
5. 若发现子立方体所分配到的单位元元素数量不为零且跟父立方体是一样的，则该子立方体停止细分，因为跟据空间分割理论，细分的空间所得到的分配必定较少，若是一样数目，则再怎么切数目还是一样，会造成无穷切割的情形。
6. 重复步骤3，直到达到最大递归深度。

八叉树在存储三维数据时能节省大量空间，特别是空间分布较稀疏的情况下。例如，通过雷达采集或者经过算法实现的三维重建都会生成PointCloud点云数据，八叉树可以实现在\(O(LogN)\)时间复杂度下的最近邻接点搜索。